
The particle size distribution, bulk density, and porosity of a compost mixture are the second group of factors that can lead to anaerobic conditions. These physical characteristics of the compost mixture can interact with high moisture levels to reduce oxygen transport. Small particle sizes reduce the number of large pores and increase the likelihood that oxygen will need to diffuse a long way through small pores (which are more likely to be filled with water, as described in the section on capillary theory and matric potential).
The shape, size, and structure of particles affects how they settle, with tight packing arrangements increasing the bulk density and reducing the air filled porosity (free air space). Compaction (caused mechanically or by the weight by overburden in tall piles) encourages tight packing as well. Several of these effects are illustrated in Figure 1 below:
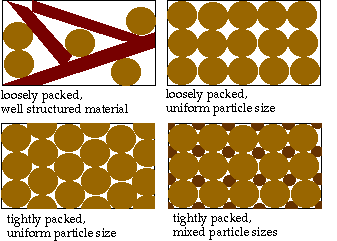
The white space between the particles in figure 1 illustrates the effective cross sectional area of each matrix. Estimates of effective cross sectional area can be used to apply the diffusion equation to a porous media like compost, correcting for the fact that diffusion only occurs in the pore space and is further constrained by tortuosity of those pores. A useful result of this correction is the apparent diffusion coefficient, which in soils has been shown to be roughly proportional to the square of the air filled porosity (Papendick and Campbell, 1981):
Deffective = S2 x D
where
Deffective = effective diffusion coefficient
S = air filled porosity, and
D = the diffusion coefficient in air
Assuming a compost matrix experiences similar effects, we can use this equation to estimate the impact of density on diffusion. Since any increase in bulk density is at the expense of the air filled porosity (the solid and aqueous phases can be considered incompressible), relatively small changes in volume can have a significant effect.
For example, suppose a pile of compost has an initial air filled porosity of 30%, and the volume of a pile is reduced by 10% through compaction and size reduction after the first pass of a windrow turner. Assuming constant moisture and solids content, the air filled porosity would be reduced from 30% to 20%, a 33% reduction [(0.30-0.20)/0.30], and the apparent diffusion coefficient will be reduced by 56% [(0.09 - 0.04)/0.09]. This significant change in oxygen diffusion might easily pass unnoticed in the windrow itself, where volume reductions of greater than 50% are common, and 80% is not unheard of with an initially loose material like autumn leaves.
To the extent that natural or forced convection is important in oxygen transport, small diameter pores can cause problems even if total air filled porosity is maintained. The increased frictional resistance from the walls in small pores reduces any mass flow of oxygen that would otherwise occur. In addition, the air channels in a composting matrix are not a bundle of continuous straight tubes, but twist and bend in tortuous path, with many dead ends and narrow passages. These factors further reduce oxygen transport in ways that are difficult to quantify.
The physical characteristics of the compost matrix affect the ease with which oxygen can move into a pile. But the distance it penetrates is also a function of how quickly it is being used up. A rapidly degrading substrate, like grass clippings or food scraps, can use up oxygen more rapidly than it is being replaced.
Reference
Papendick, R.I., and Campbell, G.S. 1981. Theory and measurement of water potential. pp 1-22. In: Water Potential Relations in Soil Microbiology. SSSA special publication No. 9. J.F. Parr, W.R. Gardner and L. F. Elliott, (eds.). Soil Science Society of America: Madison, Wis. U.S.A. Return to citation in text.
|
Composting |
Engineering |
in Schools |
|
Cornell Waste Management Institute ©1996
Cornell University
Ithaca, NY 14853
607-255-1187
cwmi@cornell.edu