Capillary Theory and Matric Potential

Tom Richard

Moisture content affects oxygen transport in several ways. The first effect of moisture content on oxygen diffusion is the increase in aqueous film thickness around individual particles in the mixture. The second effect, and the topic of this discussion, is a matrix effect, acting on the aggregate of compost particles. As moisture content increases, capillary action fills the small pores with water, often dramatically increasing the distance oxygen must diffuse through the aqueous phase. The theory that predicts these capillary effects is based on soil matric potential rather than moisture content, but these two parameters are related. Miller (1989) fit a linear relationship to data from a mixture of sewage sludge and wood chips:

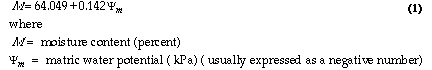
In this mixture the matric potential was zero at 64% moisture, but both this intercept and the slope may vary for different materials and mixtures. Miller (1996) also indicated that a second order polynomial (Figure 2, 1989) fit the data somewhat better than the linear relationship given. Serra-Wittling et al. (1996), working with muncipal solid waste compost, measured a matric potential of -10 kPa at 62% moisture, agreeing with Miller's result at least at high moisture contents.

If we view the compost matrix as an idealized mixture of solids and pores which take the form of capillary tubes, equilibrium between the upward forces of surface tension and the downward force of gravity will be found at:

(Bear, 1972; Weast, 1969; Kabat and Beekma, 1994 )

If we assume the fluid in the pores has the same properties as water, the matrix is a bundle of uniform tubes, and neglect other forces such as osmotic potential, we can set and solve for the radius at any given matric potential. The result, for the properties of water at 55°C, is:

The assumptions stated above make it clear that this result is greatly simplified version of reality. Nonetheless, it illustrates the dramatic effect increases in moisture have on the size of air filled pores near saturation. Combining equation (3) with Miller's (1989) relationship between moisture content and matric potential, Table 1 gives the critical air filled pore radius at a given moisture content. Pores larger than this critical dimension remain largely air filled, while smaller pores are filled with water.

Table 1. Critical Pore Radius

Moisture Content (%)	Matric Potential (kPa)	Critical pore radius (mm)
30	-239.8	0.00056
40	-169.4	0.00080
50	-98.9	0.00136
55	-63.7	0.00212
60	-28.5	0.00473
62	-14.4	0.00935
64	-0.3	0.391
64.048	-0.00007	19.2

As moisture content increases from 60 to 64%, the critical radius increases from 0.005 mm to 0.4 mm, and an additional small increase from 64 to 64.05% will saturate all pores for this particular mixture. It is important to reiterate that this example is based on Miller's (1989) relationship described in equation 1, above, and other mixtures will saturate at different moisture contents, varying between 60% to over 70% in some cases. For a compost mixture with its largest particles in the recommended range of 1.3 to 7.6 cm (Gray et al, 1971), it is easy to see that small increases in moisture content in the range near saturation will quickly fill most of the pores with water, with a corresponding reduction in the potential for diffusion to supply needed oxygen to the decomposition process.

Acknowledgement:

Marc Jalbert provided helpful comments and corrected an error in the previous version of this document (corrected Nov. 8, 2000).

References:

Bear, J. 1972. Dynamics of fluids in porous media. American Elsevier, New York. 764 pp. Return to citation in text.

Gray, K.R., K. Sherman, and A.J. Biddlestone. 1971. Review of composting. II. The practical process. Process Biochemistry 6(10):22-28. Return to citation in text.

Kabat, P., and J. Beekma. 1994. Water in the unsaturated zone. In: Drainage Principles and Applications. H.P. Ritzema (Ed.) ILRI Publication 16, 2nd Ed. International Institute for Land Reclamation and Improvement, Wageningen, The Netherlands. pp 383-434. Return to citation in text.

Miller, F.C. 1989. Matric water potential as an ecological determinant in compost, a substrate dense system. Microbial Ecology 18(1):59-71. Return to citation in text.

Miller, F.C. 1996. Personal communication. Return to citation in text.

Serra-Whittling, C., S. Houot, and E. Barriuso. 1996. Modification of soil water retention and biological properties by municipal solid waste compost. Compost Science & Utilization 4(1):44-52. Return to citation in text.

Weast, R.C. (Editor). 1969. Handbook of Chemistry and Physics, 50th Edition. Chemical Rubber Company, Inc. Cleveland, OH. p. F-30. Return to citation in text.


Cornell Composting	Science & Engineering	Composting in Schools	Resources

For specific comments related to this page, please contact the Cornell Waste Management Institute (format and style), or Tom Richard (technical content).