
Diffusion is a reflection of the fact that molecules, as they vibrate with random motion in a gas or liquid, move toward an equilibrium where all the molecular species in the mixture are uniformly dispersed, and the concentration of any one species is the same everywhere.
The diffusion equation (Fick's second law), states that the rate of molecular diffusion is proportional to the second derivative of its concentration. It its most general form this can be written:


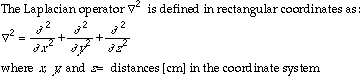
Source: Bird et al., 1960.
For a one dimensional concentration gradient of oxygen in air, this simplifies to:

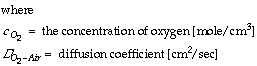
For a one dimensional concentration gradient of oxygen in water, the simplified equation is:

![]()
In a composting system, the concentration gradient is a function of the rates of oxygen supply and aerobic biodegradation and oxygen uptake (link coming soon). The O2 concentration gradient is the driving force that moves O2 into the pile by diffusion, and there is a corresponding CO2 gradient driving diffusion of CO2 out of the pile. From the practical standpoint of process management, it is the diffusion of O2 that is critical to maintaining aerobic conditions, so that will be the focus of the present analysis.
A detailed discussion is provided for calculating the oxygen diffusion coefficient in air, as well as the procedure for calculating the oxygen diffusion coefficient in water. Using this analysis, we find that the O2 diffusion coefficient in saturated air (at 15% O2 concentration) is 5700 to 10,800 times greater than in water (at 60°C and 20°C, respectively). When oxygen is forced to diffuse through water saturated pores, this restriction on oxygen transport is one of the most important factors leading to anaerobic conditions.
Reference
Bird, R.B., W.E. Stewart, and E.N. Lightfoot. 1960. Transport Phenomena. John Wiley & Sons. NY. 780 pp. Return to citation in text.
|
Composting |
Engineering |
in Schools |
|
Cornell Waste Management Institute ©1996
Cornell University
Ithaca, NY
607-255-1187
cwmi@cornell.edu