
This discussion is part of a section on oxygen transport and oxygen diffusion in compost, which provides background on the general concepts and equations.
Diffusion theory for gases is based on the kinetic molecular theory of gases, initially developed by Ludwig Boltzman and James C. Maxwell in the 19th century. This theory provides a rigorous set of equations which allow us to calculation diffusion coefficients under a wide range of conditions.
The Effects of Temperature and Pressure on Diffusion
The diffusion coefficient D is a function of both temperature and pressure. Diffusion increases with increasing temperature (as molecules move more rapidly), and decreases with increasing pressure (which packs more molecules in a given volume, making it harder for them to move). These temperature and pressure effects are illustrated by equation (1),which applies to the diffusion coefficient between any two components of a mixture (called a binary pair):
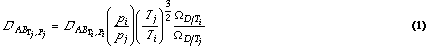

Source: Bird et al., 19601; Welty et al., 19842
For binary pairs of oxygen with nitrogen, carbon dioxide, and
water, and in the temperature range from 0°C to 80°C,
![]() ranges from about 1.3
to 3.5. Using tabulated values for
ranges from about 1.3
to 3.5. Using tabulated values for ![]() for each of the gases in the mixture (see Table 1),
for each of the gases in the mixture (see Table 1), ![]() was calculated for each binary pair according
the square root rule:
was calculated for each binary pair according
the square root rule:

Source: Welty et al., 1984
The collision integral ![]() can be approximated
from tables relating it to
can be approximated
from tables relating it to ![]() .
For the
.
For the ![]() values of interest
values of interest ![]() ranges from about 1.3 to 0.9 (decreasing as
ranges from about 1.3 to 0.9 (decreasing as ![]() increases). For this series of calculations
a 5th order polynomial was fit to the
increases). For this series of calculations
a 5th order polynomial was fit to the ![]() -
- ![]() data tabulated in appendix K1 of Welty et al.
(1984).
data tabulated in appendix K1 of Welty et al.
(1984).
For each binary pair of interest, equation (1) can then be used to calculate the binary diffusion coefficients as functions of temperature and pressure, given a diffusion coefficient measured at a known temperature and pressure. Table 1 provides the diffusion coefficients at atmospheric pressure and two temperatures for the most important constituents in an aerobic composting environment.
Table 1.
Oxygen Diffusion Coefficients of Binary Gas Pairs at Atmospheric Pressure
| Binary Pair | Temp [°C] |
[°K] |
Diffusion Coefficient [cm2/s] |
|---|---|---|---|
| Oxygen - Carbon Dioxide | 20 60 |
146 | 0.153 0.193 |
| Oxygen - Water Vapor | 20 60 |
201 | 0.240 0.339 |
| Oxygen - Nitrogen | 20 60 |
102 | 0.219 0.274 |
Mixtures of Gases
While air has relatively uniform constituency (with the exception of water vapor), the composition of gases in a compost pile varies, particularly with respect to O2 and CO2, for the reasons described above. In order to accurately calculate the O2 diffusion coefficient under these various conditions, we need to consider the relative proportions of all the gases in the mixture.
The diffusion coefficient for a mixture can be calculated from:
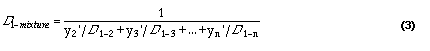

Source: Wilke (1950)3; as cited in Welty et al., 1984
Substituting the values from Table 1 in equation (3), we can calculate the diffusion constant for oxygen in a mixture of these gases, given the mole fraction of each. The results of this calculation are provided in Table 2, for variations of O2, relative humidity, and temperature. For each calculation, increases in the O2 mole fraction are assumed to be offset by CO2 increases in the calculation.
Table 2.
Effect of Temperature and Gas Mixture on Oxygen Diffusion Coefficients
| Oxygen Diffusion Coefficient [cm2/s] | |||
|---|---|---|---|
| Temperature | Relative Humidity | at 2% O2 | at 15% O2 |
| 20°C | 50% | 0.203 | 0.214 |
| 20°C | 100% | 0.203 | 0.214 |
| 60°C | 50% | 0.259 | 0.273 |
| 60°C | 100% | 0.264 | 0.278 |
From the results in Table 2 it is clear that temperature has
a much greater impact on the oxygen diffusion coefficient than
the gas mixture composition, with O2 concentration
of secondary importance and relative humidity having little effect.
It is important to remember that the oxygen concentration enters
the diffusion equation in two ways, both embedded in the diffusion
coefficient (as described above), and as the driving force through
its concentration gradient. As the driving force, oxygen concentrations
do have a very significant effect on the magnitude of diffusive
oxygen transport.
We can also estimate the oxygen diffusion coefficient in water under conditions typical of composting systems A comparison between the diffusion coefficients in these two phases illustrates why adequate air filled porosity is essential for aerobic composting.
Acknowledgment:
Jean VanderGheynst provided helpful comments and suggestions during the preparation of this document.
References:
1Bird, R.B., W.E. Stewart, and E.N. Lightfoot. 1960. Transport Phenomena. John Wiley & Sons. NY. 780 pp. Return to citation in text.
2Welty, J.R., C.E. Wicks, and R.E. Wilson. 1984. Fundamentals of Momentum, Heat, and Mass Transfer, 3rd Ed. John Wiley & Sons. NY. 803 pp. Return to citation in text.
3Wilke, C.R. 1950. Chemical Engineering Progress 46:95-104. Return to citation in text.
|
Composting |
Engineering |
in Schools |
|
Cornell Waste Management Institute ©1996
Cornell University
Ithaca, NY
607-255-1187
cwmi@cornell.edu